Тема: Системы искусственного интеллекта

1. Экспертные системы

Экспертная система – это компьютерная программа, формализующая процесс принятия решений человеком.

Экспертная система – это совокупность методов и средств организации, накопления и применения знаний для решения сложных задач в некоторой предметной области.

Назначение экспертных систем – формирование и вывод рекомендаций в зависимости от текущей ситуации, которая описывается совокупностью сведений, данных, вводимых пользователем в диалоговом режиме. Выдаваемые компьютером рекомендации должны соответствовать рекомендациям специалиста высокой квалификации.

Отличиями экспертных систем от обычных компьютерных систем являются:

· экспертные системы манипулируют знаниями, тогда как любые другие системы — данными;

· экспертные системы, как правило, дают эффективные оптимальные решения и способны иногда ошибаться, но в отличие от традиционных компьютерных систем они имеют потенциальную способность учиться на своих ошибках.

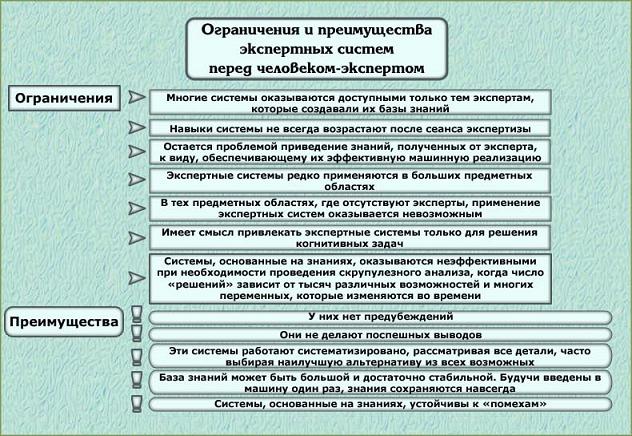
Преимущества экспертных систем по сравнению с использованием опытных специалистов состоят в следующем:

· достигнутая компетентность не утрачивается, может документироваться, передаваться, воспроизводиться и наращиваться;

· имеют место более устойчивые результаты, отсутствуют эмоциональные и другие факторы человеческой ненадежности;

· высокая стоимость разработки уравновешивается низкой стоимостью эксплуатации, возможностью копирования, а в совокупности они дешевле высококвалифицированных специалистов.

Экспертная система должна демонстрировать компетентность, т.е. достигать в конкретной предметной области того же уровня, что и специалисты-эксперты. Недостаточно находить хорошие решения, это надо делать быстро. Системы должны иметь не только глубокое, но и достаточно широкое понимание предмета. Методы нахождения решений проблем достигаются на основе рассуждений, исходящих из фундаментальных принципов в случае некорректных данных или неполных наборов правил. Такие свойства наименее разработаны в компьютерных экспертных системах, но именно они присуши специалистам высокого уровня.

Экспертная система достигает более высокой эффективности за счет перебора большого числа альтернатив при выборе решения, опираясь на высококачественный опыт группы специалистов, анализирует влияние большого объема новых факторов, оценивая их при построении стратегий, добавляя возможности прогноза.

Создание и использование экспертных систем является одним из концептуальных этапов развития информационных технологий. В основе интеллектуального решения проблем в некоторой предметной области лежит принцип воспроизведения знаний опытных специалистов — экспертов. Исходя из собственного опыта, эксперт анализирует ситуацию и распознает наиболее полезную информацию, оптимизирует принятие решений, отсекая тупиковые пути.

Искусственная компетентность экспертных систем не заменяет полностью человека. Эксперт-человек способен реорганизовать информацию и знания и использовать их для синтеза новых знаний. В области творческой деятельности люди обладают большими способностями и возможностями по сравнению с самыми умными системами. Эксперты справляются с неожиданными поворотами событий и, используя новые подходы, способны проводить аналогии из других предметных областей. Эксперты адаптируют к изменяющимся условиям и приспосабливают свои стратегии к новым обстоятельствам в более широком диапазоне проблем и задач. Экспертные системы менее приспособлены к обучению на уровне новых концепций и новых правил. Они оказываются не столь эффективны и мало пригодны в тех случаях, когда надо учитывать всю сложность реальных задач.

Эксперты могут непосредственно воспринимать весь комплекс входной информации: символьной, визуальной, графической, текстовой, звуковой, осязательной, обонятельной. У экспертной системы есть только символы, с помощью которых представлены базы знаний, воплощающие те или иные концепции. Преобразование сенсорной информации в символьную сопровождается потерей части информации.

Но главное, что огромный объем знаний, которым обладают эксперты-специалисты (профессиональные знания и знания о мире и действующих в нем законах), не удается пока встроить в интеллектуальную систему, тем более столь специализированную, какой является любая экспертная система.

Недостатком экспертных систем, характерным для их современного состояния, является меньшая приспособляемость к обучению новым правилам и концепциям, к творчеству и изобретательству. Использование экспертных систем позволяет во многих случаях отказаться от высококвалифицированных специалистов, но предполагает оставить в системе место эксперту с более низкой квалификацией. Экспертные системы служат средством для расширения и усиления профессиональных возможностей конечного пользователя. Наиболее уязвимы экспертные системы в распознавании границ своих возможностей и демонстрируют ненадежное функционирование вблизи границ их применимости. Дальнейший прогресс в области искусственного интеллекта со временем предложит способы выявления границ своих возможностей. Другим недостатком экспертных систем являются значительные трудозатраты, необходимые для пополнения базы знаний. Получение знаний от экспертов и внесение их в базу знаний представляет собой сложный процесс, сопряженный со значительными затратами времени и средств. Проектирование экспертных систем также имеет определенные трудности и ограничения, которые влияют на их разработку.

Области применения экспертных систем

Зарубежный опыт показывает, что экспертные системы разрабатываются в основном в университетах, научно-исследовательских центрах и коммерческих организациях, в том числе и для финансовой индустрии. В сфере финансового обслуживания эти системы помогают страховым компаниям анализировать и оценивать коммерческий риск, устанавливать размеры ссуд при кредитовании организаций, составлять сметы проектов и т.д.

Но область применения экспертных систем расширяется. Кроме охвата различных областей деятельности, одним из наиболее важных последствий разработки экспертных систем является модификация знаний. По мере того как разработчики будут строить большие, сложные базы знаний, появляется рынок знаний, независимых от компьютерных систем. Появятся средства обучения для изучающих определенную прикладную область. Коммерческим продуктом станут метазнания, т.е. знания об оптимальных стратегиях и процедурах использования предметных знаний. Развитие экспертных систем в интеллектуальные состоит в слиянии концепций оборудования, средств их создания (языков) и самих экспертных систем. Объединение интеллектуальных систем особенно эффективно в сложных инфраструктурах. Интеллектуальные системы уже разрабатываются и внедряются за рубежом для коммерческого использования.

Так например, экспертная система FOLIO (Стенфордский университет, США) помогает консультантам по инвестициям определять цели клиентов и подбирать портфели ценных бумаг, наиболее соответствующие этим целям. Система определяет нужды клиента в ходе интервью и затем рекомендует, в каких пропорциях надо распределить капиталовложения между разными фондовыми инструментами, чтобы наилучшим образом удовлетворить запросы клиента. Система различает небольшое число классов ценных бумаг (например, ориентированные на дивиденды акций с невысоким уровнем риска или ориентированные на акции с высоким уровнем риска) и содержит знания о свойствах (например, годовых процентах на капитал) ценных бумаг каждого класса. В системе применена основанная на правилах схема представления знаний с прямой цепочкой рассуждений для вывода целей и схема линейного программирования для максимизации соответствия между целями и предлагаемым портфелем. Система доведена до уровня демонстрационного прототипа.

Ниже перечислены некоторые из предметных областей, в которых применяются экспертные системы:

· медицина;

· физика;

· химия;

· математика;

· электроника;

· информатика;

· космическая техника;

· инженерное дело;

· военное дело;

· метеорология;

· геология;

· сельское хозяйство;

· промышленность;

· юриспруденция;

· управление процессами;

· компьютерные системы.

Экспертные системы как инструмент в работе пользователей совершенствуют свои возможности решать трудные, неординарные задачи в ходе практической работы. Экспертные системы создаются для решения разного рода проблем, типы которых можно сгруппировать в категории (таблица 1).

Таблица 1 – Типичные категории применения экспертных систем

Категория / Предметная область	Решаемая проблема
Интерпретация	Описание ситуации по информации, поступающей от датчиков
Прогноз	Определение вероятных последствий заданных ситуаций
Проектирование	Построение конфигурации объектов при заданных ограничениях
Планирование	Определение последовательности действий
Диагностика	Выявление причин неправильного функционирования системы по результатам наблюдений
Отладка	Составление рецептов исправления неправильного функционирования системы
Ремонт	Выполнение последовательности предписанных исправлений
Наблюдение	Сравнение результатов наблюдений с ожидаемыми результатами
Мониторинг	Контроль за состоянием сложного оборудования Контроль за состоянием систем обеспечения
Обработка данных	Системы общения на естественном языке
Обучение	Диагностика, отладка и исправление поведения обучаемого
Образование	Проведение интеллектуальных тестов Обучение профессиям Профориентация
Управление	Управление поведением системы как целого Выделение целей Интеллектуальный анализ Календарное планирование работы предприятия Работа в системах документооборота Оценка квалификации сотрудников Выбор моделей прогнозирования
Промышленность	Диагностика сбоев на производстве Интеграция производственных функций Формирование проектных предложений Робототехника / системы машинного зрения Управление проектами Консультации по оплате труда
Картография	Интерпретация фотоснимков Решение географических задач
Военные системы	Поддержка технических систем Адаптивное управление Идентификация целевых объектов Обработка сигналов
Финансовая сфера	Консультирование по капиталовложениям Определение кредитных лимитов Рекомендации по стратегии приобретения собственности
Торговля	Установление торговых льгот Анализ динамики рыночных ситуаций Планирование размещения рекламы

Структурная схема экспертной системы

Основой экспертной системы является совокупность знаний (базы знаний), структурированных в целях формализации процесса принятия решений.

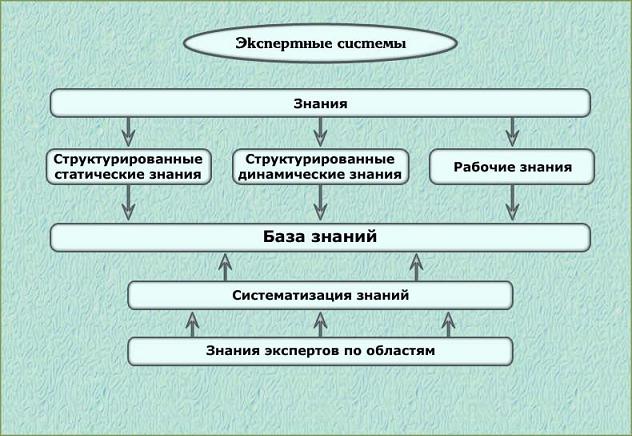
Экспертные системы разрабатываются с расчетом на обучение и способны обосновать логику выбора решения, т.е. обладают свойствами адаптивности и ее аргументирования. У большинства экспертных систем имеется механизм объяснения. Этот механизм использует знания, необходимые для объяснения того, каким образом система пришла к данному решению. Очень важным является определение области применения экспертной системы, границ ее использования и действия.

Этапы разработки экспертных систем

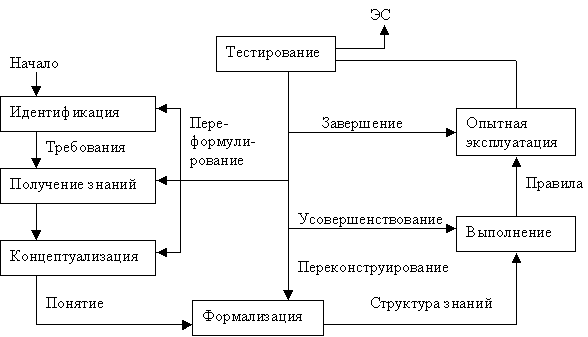
Идентификация

Этап идентификации связан прежде всего с осмыслением тех задач, которые предстоит решать будущей экспертной системе, и формированием требований к ней. На этом этапе планируется ход разработки прототипа системы, определяются источники знаний (книги, эксперты, методики), цели (распространение опыта, автоматизация рутинных действий), классы решаемых задач и т.д. Результатом этапа идентификации является ответ на вопрос, что надо сделать и какие ресурсы необходимо задействовать.

Получение знаний

При решении проблемы получения знаний используют три стратегии:

· извлечение знаний;

· приобретение знаний;

· обнаружение знаний.

Концептуализация

На этапе концептуализации проводится содержательный анализ проблемной области, выявляются используемые понятия и их взаимосвязи, определяются методы решения задач. Этот этап завершается созданием модели предметной области, включающей основные концепты и отношения. Модель представляется в виде графа, таблицы, диаграммы или текста.

Формализация

На этапе формализации все ключевые понятия и отношения выражаются на некотором формальном языке, который выбирается из числа уже существующих либо создается заново. Другими словами, на данном этапе определяются состав средств и способы представления декларативных и процедурных знаний, осуществляется это представление, и в итоге создается описание решения задачи экспертной системы на выбранном формальном языке.

Выполнение (реализация)

На этапе выполнения создается один или несколько реально работающих прототипов экспертной системы. Для ускорения этого процесса в настоящее время применяются различные инструментальные средства.

Тестирование

На данном этапе оценивается и проверяется работа программы-прототипа с целью приведения ее в соответствие с реальными запросами пользователей. Прототип проверяется по следующим основным позициям:

· удобство и адекватность интерфейсов ввода/вывода (характер вопросов в диалоге, связность выводимого текста результат и др.);

· эффективность стратегии управления (порядок перебора, использование нечеткого вывода и т.д.);

· корректность базы знаний (полнота и непротиворечивость правил).

Задача тестирования – выявление ошибок и выработка рекомендаций по доводке прототипа экспертной системы до промышленного образца.

Опытная эксплуатация

На этапе опытной эксплуатации проверяется пригодность экспертной системы для конечного пользователя. Пригодность определяется в основном удобством и полезностью разработки. Под полезностью понимается способность экспертной системы определять в ходе диалога потребности пользователя, выявлять и устранять причины неудач в работе, а также удовлетворять указанные потребности пользователя (решать поставленные задачи). В свою очередь, удобство работы подразумевает естественность взаимодействия с экспертной системой, гибкость (способность системы настраиваться на различных пользователей, а также учитывать изменения в квалификации одного и того же пользователя) и устойчивость системы к ошибкам (способность не выходить из строя при ошибочных действиях пользователя).

В ходе разработки экспертной системы всегда осуществляется ее модификация.

Выделяют следующие этапы такой модификации:

· переформулирование понятий и требований,

· переконструирование представления знаний в системе

· усовершенствование прототипа.

Усовершенствование прототипа производится в процессе циклического прохождения через этапы выполнения и тестирования для отладки правил и процедур вывода. Циклы повторяются до тех пор, пока система не будет вести себя ожидаемым образом. Изменения, осуществляемые при усовершенствовании, зависят от выбранного способа представления знаний и класса решаемых задач. Если в процессе усовершенствования желаемое поведение не достигается, то производят более серьезные модификации архитектуры системы и используемой базы знаний.

Возврат от этапа тестирования на этап формализации приводит к пересмотру ранее выбранного способа представления знаний. Данный цикл называется переконструированием.

Если возникшие проблемы еще более серьезны, то после неудачи на этапе тестирования может потребоваться возврат на этапы концептуализации и даже идентификации. В этом случае речь идет о переформулировании системы понятий, метапонятий и семантических отношений, т.е. о проектировании системы заново.

2. Нейронные сети

Биологический нейрон

Нервная система и мозг человека состоят из нейронов, соединенных между собой нервными волокнами. Нервные волокна способны передавать электрические импульсы между нейронами. Все процессы передачи раздражений от кожи, ушей и глаз к мозгу, процессы мышления и управления действиями – все это реализовано в живом организме как передача электрических импульсов между нейронами.

Нейрон (нервная клетка) является особой биологической клеткой, которая обрабатывает информацию (рисунок 1). Он состоит из тела (cell body), или сомы (soma), и отростков нервных волокон двух типов – дендритов (dendrites), по которым принимаются импульсы, и единственного аксона (ахоn), по которому нейрон может передавать импульс. Тело нейрона включает ядро (nucleus), которое содержит информацию о наследственных свойствах, и плазму, обладающую молекулярными средствами для производства необходимых нейрону материалов. Нейрон получает сигналы (импульсы) от аксонов других нейронов через дендриты (приемники) и передает сигналы, сгенерированные телом клетки, вдоль своего аксона (передатчика), который в конце разветвляется на волокна (strands). На окончаниях этих волокон находятся специальные образования – синапсы (synapses), которые влияют на величину импульсов.

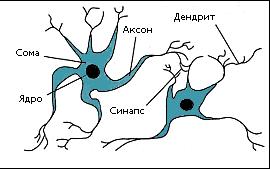
Рисунок 1 – Взаимосвязь биологических нейронов

Синапс является элементарной структурой и функциональным узлом между двумя нейронами (волокно аксона одного нейрона и дендрит другого). Когда импульс достигает синаптического окончания, высвобождаются химические вещества, называемые нейротрансмиттерами. Нейротрансмиттеры диффундируют через синаптическую щель, возбуждая или затормаживая, в зависимости от типа синапса, способность нейрона-приемника генерировать электрические импульсы. Результативность передачи импульса синапсом может настраиваться проходящими через него сигналами так, что синапсы могут обучаться в зависимости от активности процессов, в которых они участвуют. Эта зависимость от предыстории действует как память, которая, возможно, ответственна за память человека. Важно отметить, что веса синапсов могут изменяться со временем, а значит, меняется и поведение соответствующих нейронов.

Кора головного мозга человека содержит около 1011 нейронов и представляет собой протяженную поверхность толщиной от 2 до 3 мм с площадью около 2200 см². Каждый нейрон связан с 103-104 другими нейронами. В целом мозг человека содержит приблизительно от 1014 до 1015 взаимосвязей.

Нейроны взаимодействуют короткими сериями импульсов продолжительностью, как правило, несколько миллисекунд. Сообщение передается посредством частотно-импульсной модуляции. Частота может изменяться от нескольких единиц до сотен герц, что в миллион раз медленнее, чем быстродействующие переключательные электронные схемы. Тем не менее сложные задачи распознавания человек решает за несколько сотен миллисекунд. Эти решения контролируются сетью нейронов, которые имеют скорость выполнения операций всего несколько миллисекунд. Это означает, что вычисления требуют не более 100 последовательных стадий. Другими словами, для таких сложных задач мозг «запускает» параллельные программы, содержащие около 100 шагов. Рассуждая аналогичным образом, можно обнаружить, что количество информации, посылаемое от одного нейрона другому, должно быть очень малым (несколько бит). Отсюда следует, что основная информация не передается непосредственно, а захватывается и распределяется в связях между нейронами.

Искусственный нейрон

Первая формальная модель искусственного нейрона была предложена в 1943 году известным американским физиологом Уорреном Мак-Каллоком и его учеником Вальтером Питтсом. Тогда же ими было сформулировано фундаментальное утверждение о том, что любая функция нервной системы, которая может быть логически описана с помощью конечного числа слов, может быть реализована сетью искусственных нейронов.

Модель искусственного нейрона представлена на рисунке 2.

Нейрон получает входные сигналы посредством входных связей (синапсов) с определенными весовыми коэффициентами Wi. Объект-сумматор (или net в некоторых литературных источниках) определяет взвешенную сумму входных величин As. F(As) – нелинейная функция, выбираемая в значительной степени произвольно.

Рисунок 2 – Модель нейрона

Этапы развития теории нейронных сетей

1943 г. У. Маккалох (W. McCulloch) и У. Питтс (W. Pitts) предложили модель нейрона и сформулировали основные положения теории функционирования головного мозга.

1949 г. Д. Хебб (D. Hebb) высказал идеи о характере соединений нейронов мозга и их взаимодействии (клеточные ансамбли, синаптическая пластичность). Впервые предложил правила обучения нейронной сети.

1957 г. Ф. Розенблатт (F. Rosenblatt) разработал принципы организации и функционирования персептронов, предложил вариант технической реализации первого в мире нейрокомпьютера Mark.

1959 г. Д. Хьюбел (D, Hubel) и Т. Визель (Т. Wiesel) показали распределенный и параллельный характер хранения и обработки информации в биологических нейронных сетях.

1960-1968 гг. Активные исследования в области искусственных нейронных сетей, например, АДАЛИНА и МАДАЛИНА В. Уидроу (W. Widrow) (1960-1962 гг.), ассоциативные матрицы К. Штайнбуха (К. Steinbuch) (1961 г.).

1969 г. Публикация книги М. Минского (М. Minsky) и С. Пей-перта (S. Papert) «Персептроны», в которой доказывается принципиальная ограниченность возможностей персептронов. Угасание интереса к искусственным нейронным сетям.

1970-1976 гг. Активные разработки в области персептронов в СССР (основные заказчики – военные ведомства).

Конец 1970-х гг. Возобновление интереса к искусственным нейронным сетям как следствие накопления новых знаний о деятельности мозга, а также значительного прогресса в области микроэлектроники и компьютерной техники.

1982-1985 гг. Дж. Хопфилд (J. Hopfield) предложил семейство оптимизирующих нейронных сетей, моделирующих ассоциативную память.

1985 г. Появление первых коммерческих нейрокомпьютеров, например, Mark III фирмы TRW (США).

1987 г. Начало широкомасштабного финансирования разработок в области ИНС и НК в США, Японии и Западной Европе (японская программа «Human Frontiers» и европейская программа «Basic Research in Adaptive Intelligence and Neurocomputing»).

1989 г. Разработки и исследования в области ИНС и НК ведутся практически всеми крупными электротехническими фирмами. Нейрокомпьютеры становятся одним из самых динамичных секторов рынка (за два года объем продаж вырос в пять раз). Агентством DARPA (Defence Advanced Research Projects Agency) министерства обороны США начато финансирование программы по созданию сверхбыстродействующих образцов НК для разнообразных применений.

1990 г. Активизация советских исследовательских организаций в области ИНС и НК (Институт кибернетики им. Глушкова в Киеве, Институт многопроцессорных вычислительных систем в Таганроге, Институт нейрокибернетики в Ростове-на-Дону). Общее число фирм, специализирующихся в области ИНС и НК, достигает трехсот.

1991 г. Годовой объем продаж на рынке ИНС и НК приблизился к 140 млн. долларам. Создаются центры нейрокомпьютеров в Москве, Киеве, Минске, Новосибирске, С.-Петербурге.

1992 г. Работы в области ИНС находятся стадии интенсивного развития. Ежегодно проводится десятки международных конференций и форумов по нейронным сетям, число специализированных периодических научных изданий по указанной тематике достигло двух десятков наименований.

1996 г. Число международных конференций по ИНС и НК достигло ста.

1997 г. Годовой объем продаж на рынке ИНС и НК превысил 2 млрд. долларов, а ежегодный прирост составил 50%.

2000 г. Переход на субмикронные и нанотехнологии, а также успехи молекулярной и биомолекулярной технологии приводят к принципиально новым архитектурным и технологическим решениям по созданию нейрокомпьютеров.

Искусственные нейронные сети

В 50-60 годы группой ученых были созданы первые искусственные нейронные сети (ИНС), путем объединения биологических и физиологических подходов в процессе их моделирования. Реализованные первоначально как электронные сети, позднее они были перенесены и адаптированы в компьютерных средах моделирования, где активно исследуются и сегодня. В этот период активно работают многие выдающиеся ученые в области ИНС: М. Минский, Ф. Розенблатт, Б. Уидроу и др. Ими изучаются и разрабатываются ИНС, состоящие из одного слоя искусственных нейронов с обучением, называемые перцептронами (персептронами), широкое применение которых позволило получить качественно новые результаты при решении таких задач, как предсказание погоды, анализ электрокардиограмм, искусственное зрение. Несколько наиболее активных ученых, таких, как Т. Кохонен, С. Гроссберг, Дж. Андерсон развили и продолжили исследования в 70-80 годы. Сегодня существует много практических примеров, демонстрирующих впечатляющие возможности ИНС: их научили превращать текст в фонетическое представление, которое затем превращается в речь; другие ИНС могут распознавать рукописные буквы, сжимать изображения и т.д.

Под искусственными нейронными сетями (ИНС) подразумеваются вычислительные структуры, которые моделируют простые биологические процессы, обычно ассоциируемые с процессами человеческого мозга. Они представляют собой распределенные и параллельные системы, способные к адаптивному обучению путем анализа положительных и отрицательных воздействий. Элементарным преобразователем в данных сетях является искусственный нейрон или просто нейрон, названный так по аналогии с биологическим прототипом.

Искусственные нейронные сети строятся по принципам организации и функционирования их биологических аналогов. Они способны решать широкий круг задач распознавания образов, идентификации, прогнозирования, оптимизации, управления сложными объектами. Дальнейшее повышение производительности компьютеров все в большой мере связывают с ИНС, в частности, с нейрокомпьютерами (НК), основу которых составляет искусственная нейронная сеть.

Нейронная сеть представляет собой совокупность нейроподобных элементов, определенным образом соединенных друг с другом и с внешней средой с помощью связей, определяемых весовыми коэффициентами. В зависимости от функций, выполняемых нейронами в сети, можно выделить три их типа:

· входные нейроны, на которые подается вектор, кодирующий входное воздействие или образ внешней среды; в них обычно не осуществляется вычислительных процедур, а информация передается с входа на выход путем изменения их активации;

· выходные нейроны, выходные значения которых представляют выходы нейронной сети; преобразования в них осуществляются по выражениям (1.1) и (1.2);

· промежуточные нейроны, составляющие основу нейронных сетей, преобразования в которых выполняются также по выражениям (1.1) и (1.2).

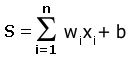(1.1)

y = f(s) (1.2)

где wi, – вес (weight) синапса, i = 1...n;

b – значение смещения (bias);

s – результат суммирования (sum);

x, – компонент входного вектора (входной сигнал),

xi = 1...n; у – выходной сигнал нейрона;

n – число входов нейрона;

f – нелинейное преобразование (функция активации).

На входной сигнал (s) нелинейный преобразователь отвечает выходным сигналом f(s), который представляет собой выход у нейрона.

Примеры активационных функций представлены в таблице 1 и на рисунке 3.

Таблица 1 – Функции активации нейронов

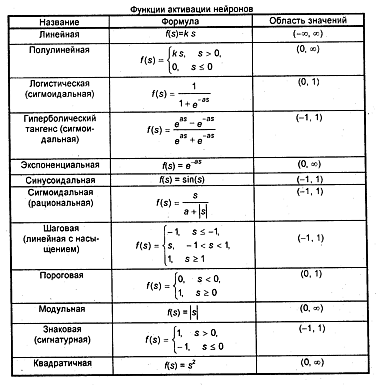
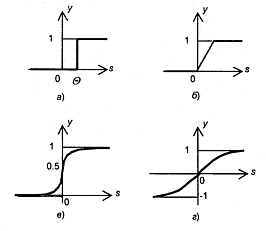
Рисунок 3 – Примеры активационных функций

а – функция единичного скачка; б – линейный порог (гистерезис);

в – сигмоид (логистическая функция); г – сигмоид (гиперболический тангенс)

Одной из наиболее распространенных является нелинейная функция активации с насыщением, так называемая логистическая функция или сигмоид (функция S-образного вида): f (s) = 1 / (1+e-as).

При уменьшении а сигмоид становится более пологим, в пределе при а = 0 вырождаясь в горизонтальную линию на уровне 0,5, при увеличении а сигмоид приближается к виду функции единичного скачка с порогом 0. Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне (0, 1). Одно из ценных свойств сигмоидальной функции – простое выражение для ее производной, что важно при реализации процесса обучения нейронной сети: f '(s) = a f(s)[1-f(s)]. Следует отметить, что сигмоидальная функция дифференцируема на всей оси абсцисс, что используется в некоторых алгоритмах обучения. Кроме того, она обладает свойством усиливать слабые сигналы лучше, чем большие, и предотвращает насыщение от больших сигналов, так как они соответствуют областям аргументов, где сигмоид имеет пологий наклон.

Проблемы, решаемые искусственными нейронными сетями

Первоначально нейронные сети предполагалось использовать для моделирования деятельности человеческого мозга, однако в настоящее время они получили широкое применение и в технике. Искусственный интеллект (на основе искусственных нейронных сетей – artificial neural networks) обладает ценными «качествами» (универсальность, высокое быстродействие, способность к обучению, устойчивость к отказам) и используется для решения многих неформализуемых или трудно формализуемых задач:

· распознавания образов;

· распознавания и синтеза речи;

· распознавания аэрокосмических изображений;

· обработки сигналов при наличии больших шумов;

· прогнозирования;

· оптимизации;

· прогнозирования котировки ценных бумаг и курса валют;

· предупреждения мошенничества с кредитными карточками;

· оценки стоимости недвижимости;

· оценки финансового состояния предприятий и риска невозврата кредитов;

· обработки радиолокационных сигналов;

· контроля движения на скоростных автомагистралях и железных дорогах;

· диагностики в медицине;

· добычи знаний из больших объемов данных в бизнесе, финансах и научных исследованиях;

· управления в реальном времени.

Классификация образов. Задача состоит в указании принадлежности входного образа, представленного вектором признаков, одному или нескольким предварительно определенным классам. К известным приложениям относятся распознавание букв, распознавание речи, классификация сигнала электрокардиограммы, классификация клеток крови.

Кластеризация/категоризация. При решении задачи кластеризации, которая известна также как классификация образов без учителя, отсутствует обучающая выборка с метками классов. Алгоритм кластеризации основан на подобии образов и размещает близкие образы в один кластер. Известны случаи применения кластеризации для извлечения знаний, сжатия данных и исследования свойств данных.

Аппроксимация функций. Предположим, что имеется обучающая выборка ((X1, Y2), (X2, Y2), ..., (XN, YN)), которая генерируется неизвестной функцией, искаженной шумом. Задача аппроксимации состоит в нахождении оценки этой функции.

Предсказание/прогноз. Пусть заданы N дискретных отсчетов {y(t1),y(t2), ..., y(tn)} в последовательные моменты времени t1, t2, ..., tn. Задача состоит в предсказании значения y(tn+1) в момент tn+1. Прогноз имеют значительное влияние на принятие решений в бизнесе, науке и технике.

Оптимизация. Многочисленные проблемы в математике, статистике, технике, науке, медицине и экономике могут рассматриваться как проблемы оптимизации. Задачей оптимизации является нахождение решения, которое удовлетворяет системе ограничений и максимизирует или минимизирует целевую функцию.

Память, адресуемая по содержанию. В модели вычислений фон Неймана обращение к памяти доступно только посредством адреса, который не зависит от содержания памяти. Более того, если допущена ошибка в вычислении адреса, то может быть найдена совершенно иная информация. Память, адресуемая по содержанию, или ассоциативная память, доступна по указанию заданного содержания. Содержимое памяти может быть вызвано даже по частичному или искаженному содержанию. Ассоциативная память чрезвычайно желательна при создании перспективных информационно-вычислительных систем.

Управление. Рассмотрим динамическую систему, заданную совокупностью {u(t), y(t)}, где u(t) является входным управляющим воздействием, a y(t) – выходом системы в момент времени f. В системах управления с эталонной моделью целью управления является расчет такого входного воздействия u(f), при котором система следует по желаемой траектории, диктуемой эталонной моделью.

Классификация искусственных нейронных сетей

Нейронные сети различают по:

· структуре сети (связей между нейронами);

· особенностям модели нейрона;

· особенностям обучения сети.

По структуре нейронные сети можно разделить (рисунок 4) на:

· неполносвязные (или слоистые) и полносвязные;

· со случайными и регулярными связями;

· с симметричными и несимметричными связями.

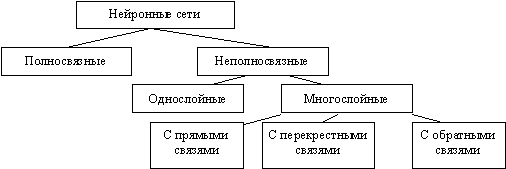
Рисунок 4 – Классификация нейронных сетей по структуре

Неполносвязные нейронные сети (описываемые неполносвязным ориентированным графом и обычно называемые перцептронами), подразделяются на однослойные (простейшие перцептроны) и многослойные, с прямыми, перекрестными и обратными связями. В нейронных сетях с прямыми связями нейроны j-ого слоя по входам могут соединяться только с нейронами i-ых слоев, где j > i , т.е. с нейронами нижележащих слоев. В нейронных сетях с перекресными связями допускаются связи внутри одного слоя, т.е. выше приведенное неравенство заменяется на j > = i . В нейронных сетях с обратными связями используются и связи j-ого слоя по входам с i-ым при j < i.

С точки зрения топологии можно выделить три основных типа нейронных сетей:

· полносвязные (рисунок 5, а);

· многослойные или слоистые (рисунок 5, б);

· слабосвязные (с локальными связями) (рисунок 5, в).

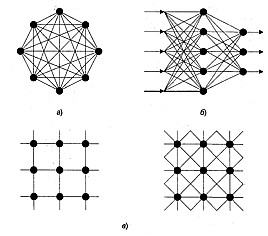
Рисунок 5 – Архитектуры нейронных сетей:

а – полносвязная сеть, б – многослойная сеть с последовательными связями, в – слабосвязные сети

В полносвязных нейронных сетях каждый нейрон передает свой выходной сигнал остальным нейронам, в том числе и самому себе. Все входные сигналы подаются всем нейронам. Выходными сигналами сети могут быть все или некоторые выходные сигналы нейронов после нескольких тактов функционирования сети.

В многослойных нейронных сетях нейроны объединяются в слои. Слой содержит совокупность нейронов с едиными входными сигналами. Число нейронов в слое может быть любым и не зависит от количества нейронов в других слоях. В общем случае сеть состоит из Q слоев, пронумерованных слева направо. Внешние входные сигналы подаются на входы нейронов входного слоя (его часто нумеруют как нулевой), а выходами сети являются выходные сигналы последнего слоя. Кроме входного и выходного слоев в многослойной нейронной сети есть один или несколько скрытых слоев. Связи от выходов нейронов некоторого слоя q к входам нейронов следующего слоя (q+1) называются последовательными.

В свою очередь, среди многослойных нейронных сетей выделяют следующие типы.

1) Монотонные. Это частный случай слоистых сетей с дополнительными условиями на связи и нейроны. Каждый слой кроме последнего (выходного) разбит на два блока: возбуждающий и тормозящий. Связи между блоками тоже разделяются на тормозящие и возбуждающие. Если от нейронов блока А к нейронам блока В ведут только возбуждающие связи, то это означает, что любой выходной сигнал блока является монотонной неубывающей функцией любого выходного сигнала блока А. Если же эти связи только тормозящие, то любой выходной сигнал блока В является невозрастающей функцией любого выходного сигнала блока А. Для нейронов монотонных сетей необходима монотонная зависимость выходного сигнала нейрона от параметров входных сигналов.

2) Сети без обратных связей. В таких сетях нейроны входного слоя получают входные сигналы, преобразуют их и передают нейронам первого скрытого слоя, и так далее вплоть до выходного, который выдает сигналы для интерпретатора и пользователя. Если не оговорено противное, то каждый выходной сигнал q-гo слоя подастся на вход всех нейронов (q+1)-гo слоя; однако возможен вариант соединения q-гo слоя с произвольным (q+p)-м слоем.

Среди многослойных сетей без обратных связей различают полносвязанные (выход каждого нейрона q-гo слоя связан с входом каждого нейрона (q+1)-гo слоя) и частично полносвязанные. Классическим вариантом слоистых сетей являются полносвязанные сети прямого распространения (рисунок 6).

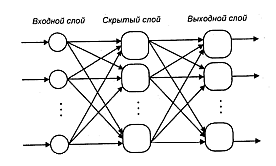
Рисунок 6 – Многослойная (двухслойная) сеть прямого распространения

3) Сети с обратными связями. В сетях с обратными связями информация с последующих слоев передается на предыдущие. Среди них, в свою очередь, выделяют следующие:

· слоисто-циклические, отличающиеся тем, что слои замкнуты в кольцо: последний слой передает свои выходные сигналы первому; все слои равноправны и могут как получать входные сигналы, так и выдавать выходные;

· слоисто-полносвязанные состоят из слоев, каждый из которых представляет собой полносвязную сеть, а сигналы передаются как от слоя к слою, так и внутри слоя; в каждом слое цикл работы распадается на три части: прием сигналов с предыдущего слоя, обмен сигналами внутри слоя, выработка выходного сигнала и передача к последующему слою;

· полносвязанно-слоистые, по своей структуре аналогичные слоисто-полносвязанным, но функционирующим по-другому: в них не разделяются фазы обмена внутри слоя и передачи следующему, на каждом такте нейроны всех слоев принимают сигналы от нейронов как своего слоя, так и последующих.

В качестве примера сетей с обратными связями на рисунке 7 представлены частично-рекуррентные сети Элмана и Жордана.

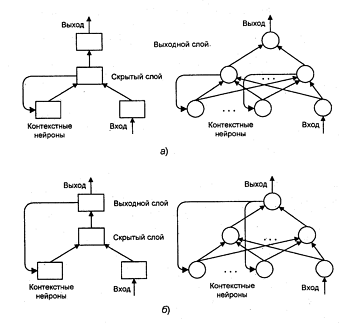
Рисунок 7 – Частично-рекуррентные сети: а – Элмана, б – Жордана

В слабосвязных нейронных сетях нейроны располагаются в узлах прямоугольной или гексагональной решетки. Каждый нейрон связан с четырьмя (окрестность фон Неймана), шестью (окрестность Голея) или восемью (окрестность Мура) своими ближайшими соседями.

Известные нейронные сети можно разделить по типам структур нейронов на:

· гомогенные (однородные);

· гетерогенные.

Гомогенные сети состоят из нейронов одного типа с единой функцией активации, а в гетерогенную сеть входят нейроны с различными функциями активации.

Еще одна классификация делит нейронные сети на:

· синхронные;

· асинхронные.

В первом случае в каждый момент времени лишь один нейрон меняет свое состояние, во втором – состояние меняется сразу у целой группы нейронов, как правило, у всего слоя. Алгоритмически ход времени в нейронных сетях задается итерационным выполнением однотипных действий над нейронами.

По используемым на входах и выходах сигналам нейронные сети можно разделить на:

· аналоговые;

· бинарные.

Бинарные оперируют только двоичными сигналами, и выход каждого нейрона может принимать значение либо логического ноля (заторможенное состояние) либо логической единицы (возбужденное состояние).

По моделированию времени нейронные сети подразделяются на сети:

· с непрерывным временем;

· с дискретным временем.

Для программной реализации применяется как правило дискретное время.

По способу подачи информации на входы нейронной сети различают:

· подачу сигналов на синапсы входных нейронов;

· подачу сигналов на выходы входных нейронов;

· подачу сигналов в виде весов синапсов входных нейронов;

· аддитивную подачу на синапсы входных нейронов.

По способу съема информации с выходов нейронной сети различают:

· съем с выходов выходных нейронов;

· съем с синапсов выходных нейронов;

· съем в виде значений весов синапсов выходных нейронов;

· аддитивный съем с синапсов выходных нейронов.

По организации обучения разделяют обучение нейронных сетей:

· с учителем (supervised neural networks);

· без учителя (nonsupervised).

При обучении с учителем предполагается, что есть внешняя среда, которая предоставляет обучающие примеры (значения входов и соответствующие им значения выходов) на этапе обучения или оценивает правильность функционирования нейронной сети и в соответствии со своими критериями меняет состояние нейронной сети или поощряет (наказывает) нейронную сеть, запуская тем самым механизм изменения ее состояния.

По способу обучения разделяют обучение:

· по входам

· по выходам.

При обучении по входам обучающий пример представляет собой только вектор входных сигналов, а при обучении по выходам в него входит и вектор выходных сигналов, соответствующий входному вектору.

По способу предъявления примеров различают:

· предъявление одиночных примеров

· предъявление "страницы" примеров.

В первом случае изменение состояния нейронной сети (обучение) происходит после предъявления каждого примера. Во втором – после предъявления "страницы" (множества) примеров на основе анализасразу их всех.

Под состоянием нейронной сети, которое может изменяться, обычно понимается:

· веса синапсов нейронов (карта весов – map) (коннекционистский подход);

· веса синапсов и пороги нейронов (обычно в этом случае порог является более легко изменяемым параметром, чем веса синапсов);

· установление новых связей между нейронами (свойство биологических нейронов устанавливать новые связи и ликвидировать старые называется пластичностью).

По особенностям модели нейрона различают нейроны с разными нелинейными функциями:

· пороговой ;

· экспоненциальной сигмоидой ;

· рациональной сигмоидой ;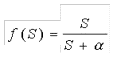

· гиперболическим тангенсом .

Перечисленные функции относятся к однопараметрическим.

Также используются многопараметрические передаточные функции, например, .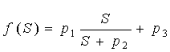

Наиболее распространенные модели нейронных сетей:

· модель Хопфилда;

· машина Больцмана;

· сеть Кохонена;

· модель Хэмминга;

· многослойный персептрон.

Модель Хопфилда

Модель разработана Хопфилдом в 1984 году. С тех пор были предложены многочисленные ее модификации. Данная модель используется как ассоциативная память, классификатор и для решения некоторых задач оптимизации.

Одна из первых предложенных моделей сети Хопфилда используется как ассоциативная память. Исходными данными для расчета значений синаптических весов сети являются векторы – образцы классов. Сеть функционирует циклически. Выход каждого из нейронов подается на входы всех остальных нейронов. Нейроны сети имеют жесткие пороговые функции.

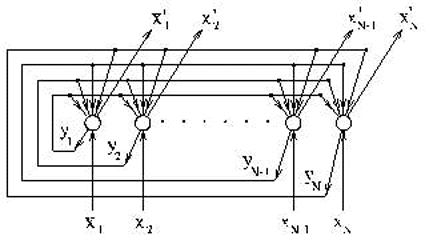
Рисунок 8 – Сеть Хопфилда

Ниже используются следующие условные обозначения:

w_ij – i-й синаптический вес j-го нейрона,

x_i – i-й элемент входного сигнала сети,

x_ij – i-й элемент j-го вектора-образца,

x_i – i-й элемент выходного сигнала сети,

y_j – выход j-го нейрона,

N – количество элементов (размерность) входного сигнала, количество нейронов в сети,

M – количество векторов-образцов.

Состояние сети характеризуется симметричной матрицей весов синапсов

Входные и выходные сигналы биполярные и принимают значения -1 и +1. Размерности входа и выхода ограничены при программной реализации только возможностями вычислительной системы, на которой моделируется нейронная сеть, при аппаратной реализации – технологическими возможностями. Размерности входных и выходных сигналов совпадают.

Сеть, содержащая N нейронов может запомнить не более M=0.15*N образов. При этом запоминаемые образы не должны быть сильно коррелированы. Мера коррелированности:

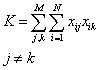
Тип передаточной функции: жесткая пороговая.

Число синапсов в сети: M*(M-1).

Формирование синаптических весов сети осуществляется по формуле:

Другими словами, веса после предъявления каждого примера вычисляются по формуле (правила Хебба):

Функционирование сети описывается следующими формулами:

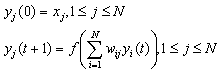
Функционирование заканчивается, если на некотором шаге T для всех j:

Нелинейная функция f обычно выглядит как пороговая, принимающая значения 1 при аргументе >0 и –1 – в противном случае. Если используются значения 0 и 1 для кодирования состояний нейронов, то сравнение производится не с нулем, а с порогом – константой, одинаковой для всех нейронов. Выходной сигнал сети:

В процессе функционирования может использоваться процедура “замораживания” состояний некоторых нейронов, которые рассматриваются как входные (т.е. на которые поступает входной сигнал). “Замороженные” нейроны не меняют своего состояния. Такое функционирование может рассматриваться как восстановление вектора по его фрагменту, а обученная нейронная сеть Хопфилда – как ассоциативная память.

В процессе функционирования уменьшается энергетическая функция:

Другими словами, состояние нейронной сети “скатывается” в минимум гиперповерхности, сформированной в процессе обучения.

Существует много разновидностей модели Хопфилда, например, с отжигом, т.е. после детерминированного алгоритма функционирования, описанного выше, работает так называемый “алгоритм отжига”, обеспечивающий уточнение решения с использованием случайного процесса, подобного ниже описанному в машине Больцмана. Этот механизм “отжига” обеспечивает возможность сети выбраться из локального экстремума энергетической функции и перейти в глобальный экстремум.

Машина Больцмана

Машина Больцмана была предложена и исследовалась во второй половине 1980-х годов. Эту модель можно рассматривать как разновидность модели Хопфилда, характеризующуюся стохастическим поиском глобального экстремума функции энергии при обучении и при распознавании входного вектора.

Этапы обучения машины Больцмана:

1. Определить переменную T, представляющую искусственную температуру.

2. Предъявить сети множество входов и вычислить выходы и целевую функцию.

3. Дать случайное изменение весу и пересчитать выход сети и изменение целевой функции в соответствии со сделанным изменением веса.

4. Если целевая функция улучшилась (уменьшилась), то сохранить изменение веса.

Если изменение веса приводит к увеличению целевой функции, то вероятность сохранения этого изменения вычисляется с помощью распределения Больцмана:

где P(c) – вероятность изменения c в целевой функции;

k – константа, аналогичная константе Больцмана, выбираемая в зависимости от задачи;

T – искусственная температура.

Выбирается случайное число r из равномерного распределения от нуля до единицы.

Если P(c) больше, чем r, то изменение сохраняется, в противном случае величина веса возвращается к предыдущему значению. Эта процедура дает возможность системе делать случайный шаг в направлении, портящим целевую функцию, позволяя ей тем самым вырываться из локальных минимумов.

Шаги 3 и 4 повторяются для каждого из весов сети, постепенно уменьшая температуру T, пока не будет достигнуто допустимо низкое значение целевой функции. В этот момент предъявляется другой входной вектор и процесс обучения повторяется. Сеть обучается на всех векторах обучающего множества, пока целевая функция не станет допустимой для всех из них.

Скорость уменьшения температуры должна быть обратно пропорциональна логарифму времени. При этом сеть сходится к глобальному минимуму.

Недостатком модели является медленный алгоритм обучения. Алгоритм дает возможность сети выбираться из локальных минимумов адаптивного рельефа.

Случайные изменения могут проводиться не только для отдельных весов, но и для всех нейронов слоя в многослойных сетях или даже для всех нейронов сети одновременно. Эти модификации алгоритма дают возможность сократить общее число итераций обучения.

При распознавании входного вектора (при тестировании сети) случайному изменению подлежат не веса связей, а состояния нейронов. Такой случайный поиск глобального экстремума может использоваться как дополнение к детерминированному алгоритму работы модели Хопфилда для уточнения полученного решения (проверки на “глобальность”)

Сеть Кохонена

Предложена Кохоненом в 1984 году. К настоящему времени существует множество модификаций исходной модели с богатой математической теорией вокруг них.

В мозге нейроны располагаются в определенном порядке так, что некоторые внешние физические воздействия вызывают ответную реакцию нейронов из определенной области мозга. Например, в той части мозга, которая отвечает за восприятие звуковых сигналов, нейроны группируются в соответствии с частотами входного сигнала, на которых они резонируют. Хотя строение мозга в значительной степени предопределяется генетически, отдельные структуры мозга формируются в процессе самоорганизации. Алгоритм Кохонена в некоторой степени напоминает процессы, происходящие в мозге. Алгоритм Кохонена дает возможность строить нейронную сеть для разделения векторов входных сигналов на подгруппы. Сеть состоит из M нейронов, образующих прямоугольную решетку на плоскости (рисунок 9). Элементы входных сигналов подаются на входы всех нейронов сети. В процессе работы алгоритма настраиваются синаптические веса нейронов.

Входные сигналы – вектора действительных чисел – последовательно предъявляются сети. Желаемые выходные сигналы не определяются. После того, как было предъявлено достаточное число входных векторов, синаптические веса сети определяют кластеры. Кроме того, веса организуются так, что топологически близкие узлы чувствительны к похожим внешним воздействиям (входным сигналам).

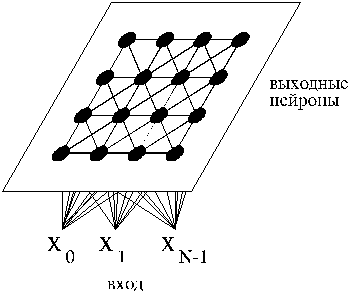
Рисунок 9 – Сеть Кохонена

Для реализации алгоритма необходимо определить меру соседства нейронов (меру близости). На рисунке 10 показаны зоны топологического соседства нейронов на карте признаков в различные моменты времени. NEj(t) – множество нейронов, которые считаются соседями нейрона j в момент времени t. Зоны соседства уменьшаются с течением времени.

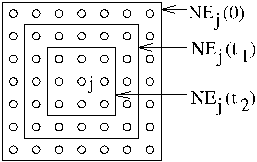
Рисунок 10 – Зоны топологического соседства

Алгоритм Кохонена формирования карт признаков:

Шаг 1. Инициализация сети: Весовым коэффициентам сети присваиваются малые случайные значения. Общее число синаптических весов – M*N (см. рисунок 9). Начальная зона соседства показана на рисунке 10.

Шаг 2. Предъявление сети нового входного сигнала.

Шаг 3. Вычисление расстояния до всех нейронов сети:

Расстояния dj от входного сигнала до каждого нейрона j определяется по формуле:

где x_i(t)- i-ый элемент входного сигнала в момент времени t,

w_ij(t) – вес связи от i-го элемента входного сигнала к нейрону j в момент времени t.

Шаг 4. Выбор нейрона с наименьшим расстоянием:

Выбирается нейрон j*, для которого расстояние dj наименьшее.

Шаг 5. Настройка весов нейрона j* и его соседей:

Производится подстройка весов для нейрона j* и всех нейронов из его зоны соседства NE. Новые значения весов:

где r(t) – шаг обучения, уменьшающийся с течением времени (положительное число, меньше единицы).

Шаг 6. Возвращение к шагу 2.

Недостатком этой модели является то, что она может быть использована для кластерного анализа только в том случае, если заранее известно число кластеров.

В отличие от сети ART Гроссберга, сеть Кохонена способна функционировать в условиях помех, так как число классов фиксировано, веса модифицируются медленно, настройка весов заканчивается после обучения (в сети ART настройка продолжается непрерывно).

Одна из модификаций состоит в том, что к сети Кохонена добавляется сеть MAXNET, которая определяет нейрон с наименьшим расстоянием до входного сигнала.

Модель Хэмминга

Расстояние Хэмминга между двумя бинарными векторами одинаковой длины – это число несовпадающих бит в этих векторах. Нейронная сеть, которая реализует параллельное вычисление расстояний Хэмминга от входного вектора до нескольких векторов- образцов, носит название сети Хэмминга.

Тип входных сигналов: бинарные векторы.

Тип выходных сигналов: целые числа.

Размерность входа и выхода ограничены при программной реализации только возможностями вычислительной системы, на которой моделируется нейронная сеть, при аппаратной реализации – технологическими возможностями. Размерности входных и выходных сигналов могут не совпадать.

Тип передаточной функции: линейная с насыщением. Число синапсов в сети: (N*M).

Рисунок 11 – Передаточная функция сети Хэмминга

Ниже используются следующие обозначения:

w_ij – i-й синаптический вес j-го нейрона, x_i – i-й элемент входного сигнала сети, y_j – выход j-го нейрона, b_j – смещение j-го нейрона, N – количество элементов (размерность) входного сигнала, M – количество нейронов в сети, – i-ый элемент j-го вектора-образца.

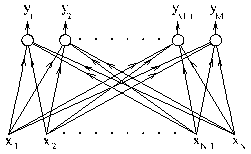
Рисунок 12 – Сеть Хэмминга

Формирование синаптических весов и смещений сети:

Функционирование сети:

Рассмотренная нейронная сеть выполняет подсчет совпадающих бит входного вектора и векторов-образцов. Синаптические веса и смещения сети, которая вычисляет расстояние Хэмминга в соответствии с данным выше определением, формируются следующим образом:

В литературе наиболее часто рассматривается модель, синаптические веса и смещения в которой вычисляются по формулам:

Области применения:

· распознавание образов;

· классификация;

· ассоциативная память;

· надежная передача сигналов в условиях помех.

Недостатки модели Хэмминга:

· сеть способна правильно распознавать (классифицировать) только слабо зашумленные входные сигналы;

· возможность использования только бинарных входных сигналов существенно ограничивает область применения.

Достоинства сети Хэмминга:

· сеть работает предельно просто и быстро, в модели использован один из самых простых алгоритмов формирования синаптических весов и смещений сети;

· выходной сигнал (решение задачи) формируется в результате прохода через всего лишь один слой нейронов (Для сравнения: в многослойных сетях сигнал проходит через несколько слоев. В сетях циклического функционирования сигнал многократно проходит через нейроны сети, причем число итераций, необходимое для получения решения, бывает заранее не известно);

· в отличие от сети Хопфилда, емкость сети Хэмминга не зависит от размерности входного сигнала, она в точности равна количеству нейронов (M) (Сеть Хопфилда с входным сигналом размерностью 100 может запомнить 10 образцов, при этом у нее будет 10000 синапсов. У сети Хемминга с такой же емкостью будет всего лишь 1000 синапсов).

Сеть Хемминга может быть дополнена сетью MAXNET, которая определяет, какой из нейронов сети Хемминга имеет выход с максимальным значением.

Многослойный персептрон и его обучение

Схема нейронной сети, получившая название многослойный персептрон(multilayer perceptron), была предложена в 1958 г. нейробиологом Ф. Розенблаттом. (рисунок 13).

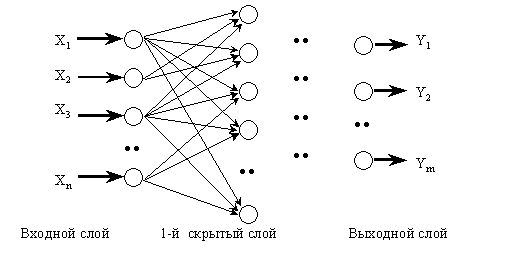
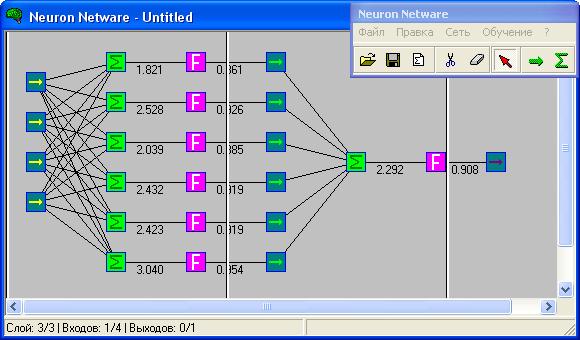
Рисунок 13 – Структурная схема многослойной нейронной сети

На структурной схеме выделены нейронные слои, включающие в себя параллельно расположенные простые узлы обработки информации – нейроны. Слой нейронов, принимающий вектор входных сигналов X, называется входным слоем (слой входов). Слой нейронов, выходные значения которых составляют выходной вектор Y, называется выходным. Остальные (промежуточные) слои называются скрытыми.

Следует отметить, что некоторые межнейронные связи в различных слоях могут отсутствовать, или иметь нулевое значение весового коэффициента связи.

Основное свойство нейронной сети – возможность изменять свои характеристики в желаемом направлении (за счет изменения весовых коэффициентов) в процессе обучения.

Целью обучения сети является такая подстройка ее весов, чтобы приложение некоторого множества входов приводило к требуемому множеству выходов. При обучении предполагается, что для каждого входного вектора существует парный ему целевой вектор, задающий требуемый выход. Вместе они называются обучающей парой. Сеть обучается на множестве пар (т.н. обучающая выборка).

Перед началом обучения всем весам должны быть присвоены небольшие начальные значения, выбранные случайным образом. Это гарантирует, что в сети не произойдет насыщения большими значениями весов, и предотвращает ряд других патологических случаев.

Один из часто используемых методов – метод обратного распространения (Back Propagation Method).

Обучение сети требует выполнения следующих операций:

1) выбрать очередную обучающую пару из обучающего множества; подать входной вектор на вход сети;

2) вычислить выход сети;

3) вычислить разность между выходом сети и требуемым выходом (целевым вектором обучающей пары);

4) подкорректировать веса сети так, чтобы минимизировать ошибку;

5) повторить шаги с 1 по 4.

3. Нечеткая логика

Пусть Х – произвольное непустое множество. Нечетким множеством (fuzzy set) А называется множество пар

где х принадлежит Х, значения m(х) лежат на отрезке [0, 1].

Функция m(х), которая отображает множество Х на отрезок [0, 1] называется функцией принадлежности нечеткого множества А, а Х называется базовым множеством или базовой шкалой.

Возможные формы задания функции принадлежности:

· графический;

· аналитический;

· табличный.

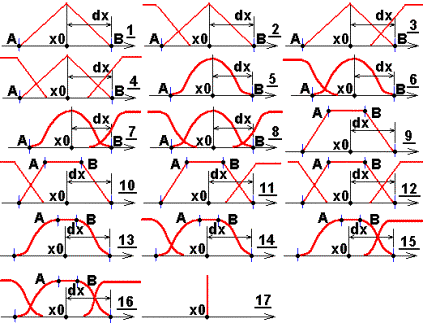
Рисунок 14 – Формы функций принадлежности:

1- треугольная, 2 – треугольная-Z типа, 3 – треугольная-S типа, 4 – треугольная-Z-S типа, 5 – колоколообразная, 6 – колоколообразная-Z типа, 7 – колоколообразная-S типа, 8 – колоколообразная-Z-S типа, 9 – трапецеидальная, 10 – трапецеидальная-Z типа, 11 – трапецеидальная-S типа, 12 – трапецеидальная-Z-S типа, 13 – трапецивидная-колоколообразная, 14 – трапецивидная-колоколообразная-Z типа, 15 – трапецивидная-колоколообразная-S типа, 16 – трапецивидная-колоколообразная-Z-S типа, 17 – точечная.

Существует ряд методов построения по экспертным оценкам функции принадлежности нечеткого множества.

Можно выделить две группы методов: прямые и косвенные.

Прямые методы определяются тем, что эксперт непосредственно задает правила определения значений функции принадлежности m_А, характеризующей понятие А. Эти значения согласуются с его предпочтениями на множестве объектов U следующим образом:

· для любых u1, u2 ÎU mА(u1)<mА(u2) тогда и только тогда, когда u2 предпочтительнее u1, т.е. в большей степени характеризуется понятием А;

· для любых u1, u2 ÎU mА(u1)=mА(u2) тогда и только тогда, когда u1 и u2 безразличны относительно понятия А.

Примеры прямых методов: непосредственное задание функции принадлежности таблицей, формулой, примером.

В косвенных методах значения функции принадлежности выбираются таких образом, чтобы удовлетворить заранее сформулированным условиям. Экспертная информация является только исходной информацией для дальнейшей обработки. Дополнительные условия могут налагаться как на вид получаемой информации, так и на процедуру обработки.

Однако функция принадлежности может отражать, как мнение группы экспертов, так и мнение одного (уникального) эксперта, следовательно, возможны, по крайней мере, четыре группы методов: прямые и косвенные для одного эксперта, прямые и косвенные для группы экспертов. Кроме того, существуют методы построения функций принадлежности терм-множеств. Классификация методов представлена на рисунке 9.

Рисунок 15 – Классификация методов построения функции принадлежности

Лингвистической переменной (linguistic variables)называется тройка <b, T, X>, где b – наименование лингвистической переменной; Т – множество ее значений (термов), представляющих наименование нечетких переменных, областью определения каждой из которых является множество Х. Например: <Стоимость, Т, [0; 5000]>, где Т={«малая», «средняя», «высокая»}.

Носителем А называется множество тех его элементов х, для которых m(х) положительна:

Носитель.

Точка перехода А – это элемент х множества А, для которого m(х)=0.5.

a-срез нечеткого множества (А_a) – множество элементов х, для которых функция принадлежности m(х) принимает значения не меньше заданного числа a (0<a<1):

Высота нечеткого множества А находится как точная верхняя грань (максимум) его функции принадлежности:

Высота .

Если высота нечеткого множества равна 1, то такое множество называется нормализованным. В том случае, когда высота нечеткого множества А меньше 1 (такое множество называется субнормальным), можно осуществить переход к нормализованному множеству путем деления его функции принадлежности m(х) на высоту .

Если носитель нечеткого множества А состоит из единственной точки х, то такое множество называется одноточечным (singleton).

Лингвистические правила – инструкции, построенные по схеме логической импликации ЕСЛИ-ТО.

Нечеткий алгоритм (fuzzy algorithm) – упорядоченное множество нечетких инструкций (правил), в формулировке которых содержаться нечеткие указания (термы).

Процесс перехода от «четкого» (т.е. измеренного) значения к его «нечеткой» интерпретации называется фаззификацией (fuzzyfication).

Логическим выводом называется процесс получения нечеткого значения результирующих переменных на основе фактических значений входных лингвистических переменных с использованием нечеткого алгоритма. В процессе логического вывода определяются уровни активности правил исходя из значений функции принадлежности переменных в условной части правила.

Наиболее известные механизмы логического вывода:

· метод Максимума-Минимума (MAX-MIN-Inference);

· метод Максимума-Произведения (MAX-Product-Inference);

При использовании логического вывода результатом выполнения лингвистических правил является некоторое нечеткое множество, описываемое результирующей функцией принадлежности.

Переход от полученного нечеткого множества к единственному четкому значению, которое и признается затем в качестве решения поставленной задачи, называется дефаззификацией (defuzzyfication).

Перечислим некоторые из наиболее известных методов дефаззификации:

а) Метод Максимума – выбирается тот элемент нечеткого множества, которые имеет наивысшую степень принадлежности этому множеству.

Если такой элемент не является единственным, т.е. функция принадлежности m_в(у) имеет несколько локальных максимумов у₁, у₂,… у_mсо значениями m_в(у₁)=m_в(у₂)=…= m_в(у_m), или если имеется максимальное «плато» между у₁ и у_m,то выбор среди элементов, имеющих наивысшую степень принадлежности множеству, осуществляется на основе определенного критерия.

б) Метод левого (правого) максимума – выбирается наименьшее (наибольшее) из чисел у₁, у₂,… у_m, имеющих наивысшую степень принадлежности нечеткому множеству.

в) Метод среднего из максимумов – в качестве искомого «четкого значения у₀ принимается среднее арифметическое координат локальных максимумов

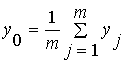г) Метод Центра Тяжести (Сenter-of-Area) – в качестве выходного значения у₀ выбирается абсцисса центра тяжести площади, расположенной под функцией принадлежности m_в(у), уÎY:

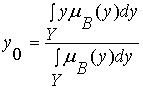При необходимости вычисления на у₀ЭВМ в реальном времени, с учетом реальных вычислительных затрат, обычно операцию интегрирования заменяют суммированием.

Существует простая возможность использования для этих целей взвешенного среднего значения

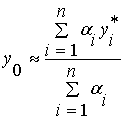где , (i=1, 2, … n) – центральные значения нечетких подмножеств В_i(у) выходной переменной у;

a_i – веса, учитывающие уровень выполнения условия «ЕСЛИ» i-го правила, называемые также уровнями активности соответствующих правил или a-уровнями;

n – число правил вывода;

д) Модифицированный метод центра тяжести – интегрирование производится только в тех областях, где m_в(у)>a, aÎ(0, 1), уÎY. Параметр a используется здесь для подавления шумов, отсеивания влияния малосущественных для процедуры вывода факторов (на практике можно применять a=0,05¸0,1).

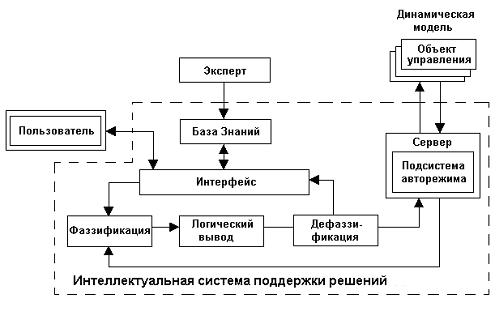
Рисунок 16 – Функциональная схема интеллектуальной системы поддержки решений, на базе алгоритмов нечеткой логики

4. Генетические алгоритмы

Генетические Алгоритмы (ГА) – адаптивные методы поиска, которые в последнее время часто используются для решения задач функциональной оптимизации. Они основаны на генетических процессах биологических организмов: биологические популяции развиваются в течении нескольких поколений, подчиняясь законам естественного отбора и по принципу "выживает наиболее приспособленный" (survival of the fittest), открытому Чарльзом Дарвином. Подражая этому процессу генетические алгоритмы способны "развивать" решения реальных задач, если те соответствующим образом закодированы. Например, ГА могут использоваться, чтобы проектировать структуры моста, для поиска максимального отношения прочности/веса, или определять наименее расточительное размещение для нарезки форм из ткани. Они могут также использоваться для интерактивного управления процессом, например на химическом заводе, или балансировании загрузки на многопроцессорном компьютере. Вполне реальный пример: израильская компания Schema разработала программный продукт Channeling для оптимизации работы сотовой связи путем выбора оптимальной частоты, на которой будет вестись разговор. В основе этого программного продукта и используются генетические алгоритмы.

Основные принципы ГА были сформулированы Голландом (Holland, 1975), и хорошо описаны во многих работах. В отличии от эволюции, происходящей в природе, ГА только моделируют те процессы в популяциях, которые являются существенными для развития. Точный ответ на вопрос: какие биологические процессы существенны для развития, и какие нет? – все еще открыт для исследователей.

В природе особи в популяции конкурируют друг с другом за различные ресурсы, такие, например, как пища или вода. Кроме того, члены популяции одного вида часто конкурируют за привлечение брачного партнера. Те особи, которые наиболее приспособлены к окружающим условиям, будут иметь относительно больше шансов воспроизвести потомков. Слабо приспособленные особи либо совсем не произведут потомства, либо их потомство будет очень немногочисленным. Это означает, что гены от высоко адаптированных или приспособленных особей будут распространятся в увеличивающемся количестве потомков на каждом последующем поколении. Комбинация хороших характеристик от различных родителей иногда может приводить к появлению "суперприспособленного" потомка, чья приспособленность больше, чем приспособленность любого из его родителя. Таким образом, вид развивается, лучше и лучше приспосабливаясь к среде обитания.

ГА используют прямую аналогию с таким механизмом. Они работают с совокупностью "особей" – популяцией, каждая из которых представляет возможное решение данной проблемы. Каждая особь оценивается мерой ее "приспособленности" согласно тому, насколько "хорошо" соответствующее ей решение задачи. Например, мерой приспособленности могло бы быть отношение силы/веса для данного проекта моста. (В природе это эквивалентно оценке того, насколько эффективен организм при конкуренции за ресурсы.) Наиболее приспособленные особи получают возможность "воспроизводит" потомство с помощью "перекрестного скрещивания" с другими особями популяции. Это приводит к появлению новых особей, которые сочетают в себе некоторые характеристики, наследуемые ими от родителей. Наименее приспособленные особи с меньшей вероятностью смогут воспроизвести потомков, так что те свойства, которыми они обладали, будут постепенно исчезать из популяции в процессе эволюции.

Так и воспроизводится вся новая популяция допустимых решений, выбирая лучших представителей предыдущего поколения, скрещивая их и получая множество новых особей. Это новое поколение содержит более высокое соотношение характеристик, которыми обладают хорошие члены предыдущего поколения. Таким образом, из поколения в поколение, хорошие характеристики распространяются по всей популяции. Скрещивание наиболее приспособленных особей приводит к тому, что исследуются наиболее перспективные участки пространства поиска. В конечном итоге, популяция будет сходиться к оптимальному решению задачи.

В настоящее время под термином "генетические алгоритмы" скрывается не одна модель, а достаточно широкий класс алгоритмов, подчас мало похожих друг от друга. Исследователи экспериментировали с различными типами представлений, операторов кроссовера и мутации, специальных операторов, и различных подходов к воспроизводству и отбору.

Хотя модель эволюционного развития, применяемая в ГА, сильно упрощена по сравнению со своим природным аналогом, тем не менее ГА является достаточно мощным средством и может с успехом применяться для широкого класса прикладных задач, включая те, которые трудно, а иногда и вовсе невозможно, решить другими методам. Однако, ГА, как и другие методы эволюционных вычислений, не гарантирует обнаружения глобального решения за полиномиальное время. ГА-мы не гарантируют и того, что глобальное решение будет найдено, но они хороши для поиска "достаточно хорошего" решения задачи "достаточно быстро". Там, где задача может быть решена специальными методам, почти всегда такие методы будут эффективнее ГА и в быстродействии и в точность найденных решений. Главным же преимуществом ГА-мов является то, что они могут применяться даже на сложных задачах, там, где не существует никаких специальных методов. Даже там, где хорошо работаю существующие методики, можно достигнуть улучшения сочетанием их с ГА.